Title (Replace it with your project title)

Whyjay Zheng, John Doe, & John Smith

Abstract

Abstract text (<100 words).

Main

Introduction

Introduction content. No code blocks allowed in this section.

sub-heading of introduction

Feel free to divide the introduction section as you like.

sub-sub-heading of introduction

Something here.

sub-heading of introduction 2

In-line Latex math: \(\hat{\textbf{a}}=(\textbf{X}^\text{T}\textbf{X}+\lambda \textbf{I})^{-1}\textbf{X}^\text{T}\textbf{y}\)

Latex math block:

\[ \arg\min\limits_{\textbf{a}} ||\textbf{y} − \textbf{Xa}||_2^2 + \lambda||\textbf{a}||_2^2 \]

Inserting a figure:

Figure 1. CSRSR logo.

Results

Your results. No code blocks allowed in this section.

Making a table:

Table 1. Something about the results.

Label	Model	RMSE
Trial-1	Linear (ordinary least square)	0.678

sub-heading of results

Feel free to divide this section as you like.

Discussion

Discussion. No code blocks allowed in this section.

sub-heading of discussion

Feel free to divide this section as you like.

Conclusions

one paragraph concluding your work

Methods

Describe the data and methods. Code blocks allowed and recommended.

Though not necessary, I recommend that you upload the raw or processed data to somewhere that can be accessed directly for reproducing the work easily.

# Sample code cell

# Import modules
import numpy as np
from scipy.linalg import lstsq
import matplotlib.pyplot as plt

# Generate/Import data
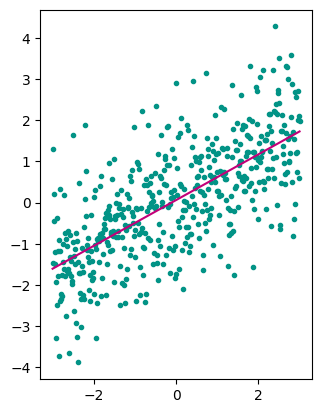
x = np.linspace(-3, 3, 500)
y = 0.5 * x + np.random.randn(500)

# Analysis
X = x[:, np.newaxis]**[0, 1]
a, _, _, _ = lstsq(X, y)
print(f'Model: y = {a[0]:.2f} + {a[1]:.2f}x')

# Visualization
plt.plot(x, y, '.', color='xkcd:teal')
plt.plot(x, np.polyval(np.flip(a), x), color='xkcd:magenta')
plt.gca().set_aspect('equal', 'box');   
# I ddded a semicolon in the end of the last line 
# to prevent unnecessary output print.

Model: y = 0.06 + 0.56x

sub-heading of methods

Feel free to divide the method section as you like.

References

1. Banks, G. C., et al. (2019). Answers to 18 Questions About Open Science Practices. Journal of Business and Psychology, 34(3), 257–270. https://doi.org/10.1007/s10869-018-9547-8 | Full text available on ResearchGate (accessed on February 16, 2023)

2. Piller, C. (2022). Blots on a field? Science, 377(6604), 358–363. https://doi.org/10.1126/science.add9993